特別WEBコラム　新型コロナウィルス禍に学ぶ応用物理 2変数を用いた感染者数推移のキネティクス解析武安光太郎，中村潤児筑波大学

1.　感染速度論の考え方

COVID-19の感染者数および死者数の情報が日々報道されている状況にあるが，本稿では，これらの数値を用いてどのように感染の状況を解析するかについて解説する．まず，感染の拡大および抑制とは速度論（キネティクス）的現象である．したがって，感染の速度論的挙動がどのような要因で決まるかを科学的に解析することは，政策や対策を講じるうえで極めて重要になる．感染の速度論は，筆者らの専門とする化学反応の速度論と類似している．化学反応では分子と分子が衝突して新たな分子が生成するが，感染は感染者が非感染者と接触して新たな感染者が生まれる．したがって，両者には数理的に同様な速度論が適用できる．ここで，速度論的解析手法には，確率論的アプローチと決定論的アプローチがある．本稿では後者の方式，すなわち速度論的モデルに基づいて微分方程式を解いてゆく方法について述べる．

さて，1つやっかいな問題がある．それは，市中にどれほどの感染者がいるかわからない状況で解析をするという点である．まず，その点から述べよう．今回のCOVID-19の場合では，9割程度は無症候者とみられている．また，報告によると，感染者（infectious case）が感染力を有して市中に滞在する平均日数は8日間である^{1), 2)}．このCOVID-19の内在的因子が速度論のパラメータとなる．大多数が無症候者で回復すると仮定すると，非感染者→感染者→回復者という過程からなるプロセスとみなされる．ここで感染の状況は，市中感染者数（N_inf）の時間的変化 dN_inf/dt（感染速度）で把握することができる．この速度は，感染者生成速度と感染者回復速度のバランス（差）で決まる．ここで時間 t の単位を日とすると，8日間で回復するということは1日に市中感染者の 1/8 が回復するということになり，感染者回復速度は 0.125 N_inf と書くことができる．一方，感染者生成速度は，人と人との接触率，密度，政策（ロックダウン，マスク，社会的距離）や感染待ち時間や発症期間などの複合的要因で決まる．さて，N_inf は不明ではあるが，ある程度の予測をすることができる．それは日々報道される新規感染者数である．先に，9割程度は無症候者と記したが，コンタクトトレーシングと呼ばれる感染者追跡を十分に行わない場合，PCR（Polymerase Chain Reaction）検査で陽性と判断される感染者は実際の感染者の1割にも満たない．そのほとんどが，自覚症状のある感染者であり，重症者が含まれ，また，その感染者との濃厚接触者（軽症者，無症候者）も付随する．したがって，非感染者→感染者→回復者という流れにおいて，日々報道される新規判明感染者（daily confirmed cases）は市中感染者のほんの一部であり，感染者生成速度をサンプリングしていると見なせる．新規感染者数自体は1日当たりの感染者数増加なので，速度と見なせ，累計判明感染者数を N_conf に対して dN_conf / dt とおける．すると，dN_inf / dt ∝ dN_conf / dt として，dN_conf / dt の速度定数の指数因子が dN_inf / dt のそれと同じになるとして，市中感染者の感染速度の増加減少を解析することが可能になる．しかし，コンタクトトレーシングを感染拡大の前に実施する場合，市中から感染者を短期間に除去できるようになり，上記の速度論を修正する必要が生じる．日本のクラスター対策班の解析は主に確率論的アプローチ（分布関数の畳み込み）であり，再生産数をより詳しく解析しているが，その再生算数変化の中身（コンタクトトレーシングの効果）に言及しているわけではない．筆者らのモデルでは，分布関数の部分は単純化して，コンタクトトレーシングを含むフローに重点をおいて解析している．今後，コンタクトトレーシングが最も重要な政策になると考えているので（論文投稿準備中），本稿でその基礎的な式を紹介したい．

2.　速度論的モデル解析

2.1　2変数モデル

はじめに，簡素化した2変数モデルを考える．感染速度は，(1)式のような速度式で表される．感染者数増減の速度である dN_inf / dt は，見かけの速度定数 k_app と感染者数 N_inf との積になっている．すなわち，感染速度は感染者数の1次に比例する．化学では1次の反応速度式と呼ばれる．感染者と非感染者の接触頻度が感染者数に比例するからである．次に，見かけの速度定数 k_app は感染速度の程度の指標である．正の値ならば感染速度は増加し，負の値ならばそれが減少する．また，k_app が 0.3 ならば感染者数が毎日 30% 増加し，-0.1 ならばそれが毎日 10% 減少する．さて，2変数モデルとは，見かけの速度定数 k_app が感染者生成の速度定数kと消滅の速度定数 k’ の2変数で決まるということである．すなわち k_app = k – k’ である．感染者1人が感染力をもつ間に1日当たりに感染させる確率（割合）を k，感染者1人が1日当たりに自然回復や入院，コンタクトトレーシングなどによって市中からいなくなる確率を k’ とおく．前述のように，k’ の逆数がちょうど感染者の市中滞在日数の平均値に対応する．また，感染者が，感染力を有する期間内に，感染させる人数が再生算数 R であるが，k / k’ がおおよそ R に対応する値になる．2変数モデルに基づくと，時間（日にち） t における感染者数 N_inf(t) についての速度式が

(dN_inf (t))/dt=k_app N_inf (t)=(k-k^')N_inf (t) (1)

と表される．さらに，k や k’ が時間に依存しないとき，変数分離法を用いて(1)式を解けば，時間（日にち） 0 における感染者数 N_inf(0) を用いて(2)式のようになる．

N_inf (t)=N_inf (0) e^kappt=N_inf (0) e^((k-k^')t) (2)

この式は感染症のモデルとして古くから知られるケルマック・マッケンドリック（Kermack-McKendrick）のモデル³⁾に対応する．(2)式を見ると，市中における感染者数の増減は，変数 k と k’ のバランスで決まることがわかる．k = k’ ならば感染者数は変化せず，k > k’ ならば指数関数的に増加，k < k’ ならば指数関数的に減少する．前述のように，k’ は感染者が市中からいなくなる速度定数である．一方，k は感染者と非感染者の接触頻度に依存し，例えばマスクの着用・手洗いの有無，社会的距離などによって変化することになる．したがって，市民の注意度が k に強く反映されることになる．以上が，感染者数がどのようにして変化するかを解析する基礎になる．

2.2　コンタクトトレーシングを組み込んだモデル

前述の2変数モデルから明らかなように，感染抑制の対策は数理的に2つに大別され，k を小さくする方式と，k’ を大きくする方式に分類される．k を小さくするロックダウンや活動自粛は経済にダメージを与えるが，k’ を大きくするコンタクトトレーシングは有効な施策として期待される．感染の問題は速度論なので，コンタクトトレーシングも時間との勝負である．すなわち，スマートフォンを利用して，軽症者や無症候者を発見し，直ちにPCR検査を受けさせ，短時間に感染経路の発見を進める体制の構築である．PCR検査チームとトレーシングチームの拡充および組織間の連絡体制の強化に加え，市民の自発的な協力が加われば，想定されるクラスター発生に十分対応が可能になる．ニュージーランド，韓国，アイスランド，ベトナムではコンタクトトレーシングが成功をおさめているが，感染が縮小している間も継続しているので，国民に安心感を与えている．これらを考慮して，SEIR（Susceptible-Exposed-Infectious-Recovered）モデル（被感染能保有者 – 感染してから感染能を有するまでの者 – 感染能保有者 – 回復者のルートを考えたモデルで，2変数モデルを一般化したもの）⁴⁾を改変したモデルの模式図を図1に示す．

図1　SEIR改変モデルのフローチャート．

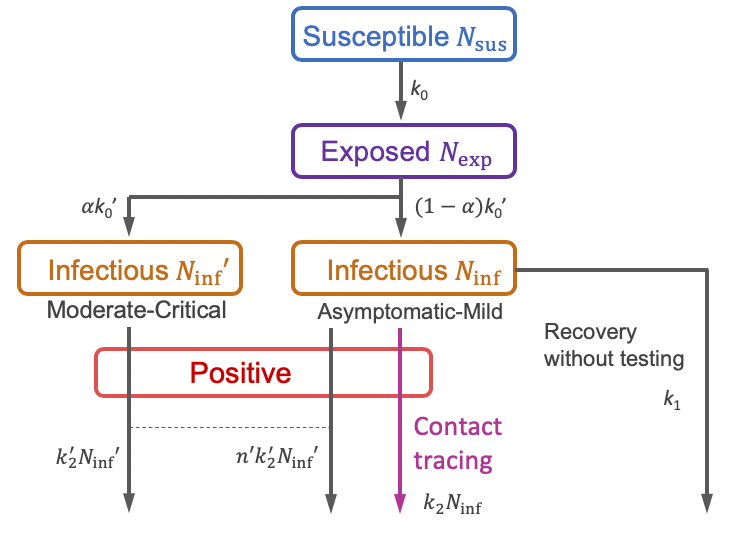
まず感染可能者（N_sus）が速度 k₀N_inf N_sus / N_tot で感染者（N_exp）となる．ここで N_tot は全人数（感染可能者，感染者，回復者，死亡者を含む）である．確率αで重症化した感染者（患者数N_inf’）は検査を受け，速度 k₂’N_inf’ で，病床数に余裕があれば入院することになる．このとき，重症化した感染者の同居人や同僚などが自動的に検査を受け，平均して n’ 人の感染者が発見されるとする．一方，ウイルスに曝（さら）されたあとに，確率（1 – α）で無症状・軽症に留まった人（N_inf 人）のうち，検査を受けることなく自然回復していく速度を k₁N_inf とおく．無症状・軽症患者は，身近に重症者がいないかぎりは自発的に検査を受けることは少なく，コンタクトトレーシングなどの積極的な施策により速度 k₂N_inf で発見されて隔離されると考える．以上の SEIR 改変モデルの速度式は(3)〜(5)式のようになる．

(〖dN〗_exp (t))/dt=k_0 N_inf (t)(N_sus (t))/N_tot -k_0'N_exp (t) (3)

(〖dN〗_inf'(t))/dt=αk_0'N_exp (t)-k_2'N_inf'(t) (4)

(〖dN〗_inf (t))/dt=(1-α) k_0^' N_exp (t)-n'k_2'N_inf'(t)-k_1 N_inf (t)-k_2 N_inf (t) (5)

N_sus 〜 N_tot のときにこれらを満たす N_inf(t) は N_inf(t) = N_inf(0)e^k_appt の形で与えられ，これを(3)式に代入すると N_exp(t) について解くことができる．次に得られた N_exp(t) を(4)式に代入すると N’_inf(t) を得る．N_inf(t)，N’_inf(t) および N_exp(t) を(5)式に代入し，N_inf(0) ≠ 0 のもとで整理すると，k_app について次の関係式を得る．

k_app=(1-α) (k_0'k_0)/(k_app+k_0^' ) -n^' k_2^' (αk_0^' k_0)/((k_app+k_2^')(K+k_0^'))-(k_1+k_2) (6)

(6)式の右辺第1項が2変数モデルの k に対応し，右辺第2項と第3項が k’ に対応する．

3.　解析方法と具体例

図1のSEIR改変モデルで，Positive（陽性者）のボックスからの流れである，日々の判明感染者数 dN_conf / dt は次式で表される．

(〖dN〗_conf (t))/dt=(n^'+1) k_2'N_inf'(t)+k_2 N_inf (t) (7)

(7)式に N_inf(t)，N’_inf(t) を代入すると

(〖dN〗_con (t))/dt=[(n^'+1) k_2^' (αk_0'k_0)/(k_app+k_2^' )(k_app+k_0^' ) +k_2 ] N_in (0) e^(k_app t) (8)

の形で dN_conf / dt が表され，指数関数の肩に k_app が現れる．また2変数モデルの場合には，日々の判明感染者数が実際の感染者数に比例するとすれば，やはり日々の判明感染者数が e^k_appt に比例する形になる．そこで，日々の判明感染者数の対数を縦軸にとり，横軸に時間（日にち）をとったグラフを作成すると，その傾きが k_app に対応する．前述のように，市中感染者の数を知らなくても，k_app が求められることが示された．

図2に東京都の日々の判明感染者数⁵⁾の対数を日付に対してプロットしたものを示す．

図2　東京都の日付に対する日々の判明感染者数の対数プロット．

図2の傾き（k_app）を見ると，緊急事態宣言が出るまでは約 0.11 となっており，緊急事態宣言の最中には最大で -0.17 程度まで下がり，緊急事態宣言の解除後は再び 0.09 まで上昇していることがわかる．k_app = 0.11という数値は，2変数モデルで粗く見た場合には，感染期間 8 日の逆数をとって k’ = 0.12 を仮定すると k = 0.23 に対応し，再生産数では2程度に対応する．ヨーロッパの人口 5000万人以上の国では，感染拡大初期の再生産数は 3〜4 程度になっており，それと比較すると東京都の再生算数は小さい値になっている．これには，東京都の施策や，個々人の衛生に対する比較的高い衛生意識が反映されているかもしれない．スウェーデンが国策で論じたように，抗体の獲得によって被感染能保有者数 N_sus が人口 N_tot に対して何割が減少すると，実効再生算数が有意に減少してくる．東京都や日本国内でも N_sus の減少による効果が話題になるが，もし N_sus が実際に小さいならば，我々の解析においてその効果は k あるいは k₀ に取り込まれ，感染速度は見かけ上小さくなる．この可能性については別途，疫学的・統計的な解析データがないと検討できないが，厚生労働省が6月16日に公表したように抗体獲得者割合が 0.1% 程度⁶⁾であるならば，N_sus の減少による影響は十分無視できるであろう．東京都のデータに戻ると，緊急事態宣言の最中の k_app = -0.17 は，再生算数が 0 に近くてかつコンタクトトレーシングなどの施策を行わないと達成できない数値であり，政策と保健所や病院などの機関の努力が反映されていると考えられる．しかしながら，緊急事態宣言の終了とともに k_app の値は 0.1 近くまで戻っており，7月に入った時点でも日々の判明感染者数は指数関数的な増大を続けている．市民1人ひとりがこうした現状を理解し，例えばスマートフォンに厚生労働省が発表している感染者接触確認用のアプリケーションを入れるなどして，意識をもって協力する体制を作っていかなくてはならない．

4.　むすび

本稿では，COVID-19の感染判明者推移のデータを単純な1次式で理解できることに焦点を当てて解説を行った．より厳密な解析には，SEIRモデルなどの数理モデルや，統計分布を反映した計算をしていくことが必要である一方，大要は2変数モデル（ケルマック・マッケンドリックモデル）によって理解することができる点が重要である．日々の判明感染者数の対数プロットから，指数関数的な感染者数推移の指数因子を知ることができ，そこから現状を分析することが可能である．特に，今後はコンタクトトレーシングの導入および解析が重要になると予測される．感染判明者数推移に関するリテラシーが広まり，協力体制の強化につながることを願う．

謝辞

投稿予定論文の共著者として貴重な情報・意見をいただいた柳沢正史教授（筑波大学），鈴木広道医師（筑波メディカルセンター病院），C.T. Campbell教授（米国ワシントン大学）に感謝します．

文献

1) X. He, E. H. Lau, P. Wu, X. Deng, J. Wang, X. Hao, Y. C. Lau, J. Y. Wong, Y. Guan, X. Tan, X. Mo, Y. Chen, B. Liao, W. Chen, F. Hu, Q. Zhang, M. Zhong, Y. Wu, L. Zhao, F. Zhang, B. J. Cowling, F. Li and G. M. Leung, Nat. Med. 26, 672 (2020).
2) S. Flaxman, S. Mishra, A. Gandy, J. T. Unwin, H. Coupland, T. A. Mellan, H. Zhu, T. Berah, J. W. Eaton, P. N. P. Guzman, N. Schmit, L. Cilloni, K. E. C. Ainslie, M. Baguelin, I. Blake, A. Boonyasiri, O. Boyd, L. Cattarino, C. Ciavarella, L. Cooper, Z. Cucunubá, G. Cuomo-Dannenburg, A. Dighe, B. Djaafara, I. Dorigatti, S. Van Elsland, R. Fitzjohn, H. Fu, K. Gaythorpe, L. Geidelberg, N. Grassly, W. Green, T. Hallett, A. Hamlet, W. Hinsley, B. Jeffrey, D. Jorgensen, E. Knock, D. Laydon, G. Nedjati-Gilani, P. Nouvellet, K. Parag, I. Siveroni, H. Thompson, R. Verity, E. Volz, P. Gt Walker, C. Walters, H. Wang, Y. Wang, O. Watson, X. Xi, P. Winskill, C. Whittaker, A. Ghani, C. A. Donnelly, S. Riley, L. C. Okell, M. A. C. Vollmer, N. M. Ferguson and S. Bhatt, Imp. Coll. London [March], 1 (2020).
3) W. O. Kermack and A. G. McKendrick, Proc. R. Soc. London. Ser. A, Contain. Pap. a Math. Phys. Character 115 [772], 700 (1927).
4) M. Y. Li and J. S. Muldowney, Math. Biosci. 125 [2], 155 (1995).
5) 東京都, 東京都新型コロナウイルス感染症対策サイト,
https://stopcovid19.metro.tokyo.lg.jp/.
6) 厚生労働省, 抗体保有調査における中和試験の結果について,
https://www.mhlw.go.jp/content/000648706.pdf.